【QC検定・実践分野解説】Pythonを利用した工程能力指数の検討

こんにちは、アドラーです！

今回は「QC検定1級論文対策シリーズ」として、「Pythonを利用した工程能力指数の検討」という記事を書きました。

私のQC検定1級の合格体験談で紹介したようにQC検定では30分で750字の作文を書く必要があり、QCの本質を理解していることが重要です。

QC検定に合格するために、SQCを中心とした数学の体系的な勉強をしている方も多いと思います。

一方で、体系的なQC知識は書籍で学ぶことはできても中々その知識を実務に適用することが難しいと感じている方も多いのではないでしょうか。

そこで今回は、製品開発を5年以上続けている研究開発職の私がQC知識を実務に応用した事例として、「Pythonを利用した工程能力指数の実践的な活用法」を紹介します。

この本質を理解して、工程能力指数の使い方を理解しながら、QC検定1級の論文問題を書くためのヒントを得ていただけると幸いです。

概要

初めに本記事の概要を示します。

Python環境が整っていなくても工程能力指数の検討ができるように記事を作りましたのでぜひ最後までご覧ください！

1. 工程能力とは「ある工程がどれだけ均一に、どれだけばらつきが小さく製品を生産できるかを示す品質的な能力」を示す。
2. データのばらつきを確認して、正規分布に近い分布をしていることを確認してから工程能力指数を確認する。
3. スモールデータを取り扱うときは、品質検査項目の重要性と照らし合わせながら、設計仕様見直しの必要性を議論する。

それでは一緒に勉強していきましょう！

工程能力指数の定義

工程能力とは「ある工程がどれだけ均一に、どれだけばらつきが小さく製品を生産できるかを示す品質的な能力」のことです。

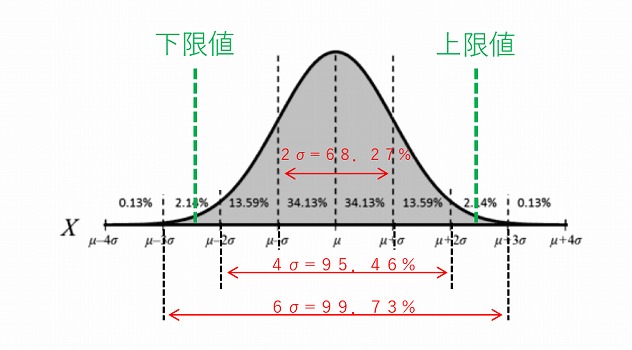
正規分布に従うデータは下記のグラフのように±3σの中に99.7%のデータが入りますが、このデータと規格幅とを比較した値を「工程能力指数」といいます。
※母集団の標準偏差をσとします。

両側規格がある場合の工程能力指数Cpは以下の式で表されます。

Cp=（規格上限−規格下限）/6σ

次に規格値が片側にしかない場合は、以下の式で表されます。

上限規格の場合

　Cp=（規格上限−平均値）/3σ

下限規格の場合

　Cp=（平均値−規格下限）/3σ

工程能力の判定方法

次に以下の表に基づいて工程能力を判断します。

Cp（Cpk）の基準	目安
Cp≧1.67	非常に優れた工程能力
1.67＞Cp≧1.33	優れた工程能力
1.33＞Cp≧1.0	まずまずの工程能力
1.0＞Cp≧0.67	不良品が多く改善が必要と判断
0.67＞Cp	数値が非常に不足しており、品質保障が困難なため是正措置が必要と判断

開発段階ではばらつきが見切れない場合がほとんどですが、コスト面で許容可能であれば性能上重要な指標についてはCp≧1.33を目指すべきでしょう。

工程能力の区間推定

新製品開発では十分なデータ数が準備できないため、区間推定を行なって工程能力のばらつきを想定します。

工程能力を区間推定する場合は以下の数式で算出します。

両側規格の場合

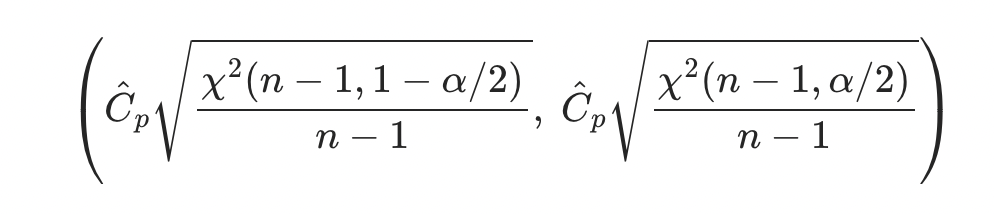
片側規格の場合

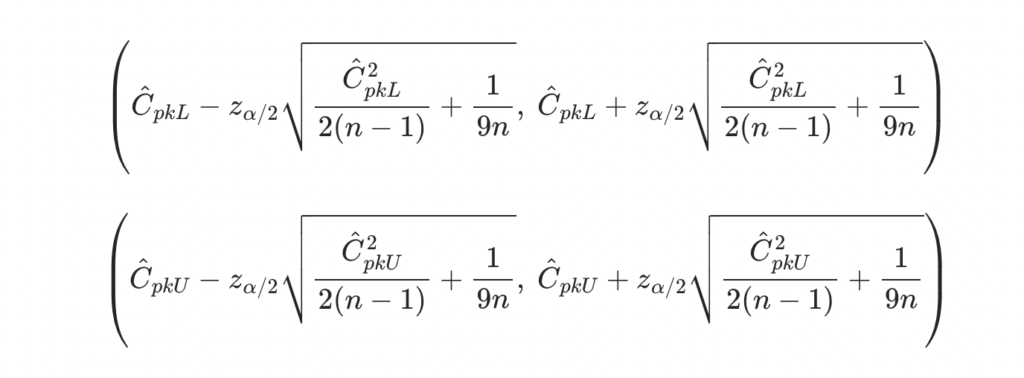
N数が少ない場合、かなりの幅で工程能力を推定されるため「ワースト想定すると大幅なコストアップをしないと目標の工程能力を達成できない」という場合が考えられます。

この場合、「QCDの観点から妥協してもOKな品質項目なのか」を考慮し、致命的な品質欠陥につながるのであれば、なるべく余裕を持った設計に変更して実力をしながら徐々にコストダウンを図るのが良いでしょう。

実践：スモールデータセットの工程能力指数

以下に研究開発で行われるようなスモールデータセットを想定して、工程能力指数を算出するためのPythonプログラムを作成しました。

③をコピペすればご自身のPython環境で実践できるので、是非ご活用ください！

①データセットの準備とPythonの設定

まずはデータの可視化と計算を行うために環境を整えます。

Python環境自体が整っていない方もいると思うので「Trinket」というサイトを用いました。

東京大学の金子邦彦先生のオープンなAI講習資料でも使用されているので、興味がある人はこちらからご覧ください。

それでは初めに計算を行うためのNumpy, pandas, seaborn, matplotlibなどの基本ライブラリをインポートします。

Trinketでは左側にある「▶︎ボタン」を押すことでプログラムを動かすことができます。

それでは「▶︎ボタン」を押してみましょう。

今回は何も表示されませんが、計算環境は整ったので特に問題はありません。

②データを可視化してデータに分布に異常がないかを確認する

データを読み込む準備ができたところでデータをヒストグラムで可視化してみましょう。

今回は正規分布に従う30個のデータをnumpyで生成して、これを検査データとして扱います。

今回は上側規格値を+4、下側規格値を-4として規格値と検査値を一緒にプロットしてみましょう。

11行目からデータフレームの作成とグラフの作成のプログラムになりますので、左側にある「▶︎ボタン」を押してみましょう。

「▶︎ボタン」を押してコードを動かしてみるとグラフを表示できました。

N数が少ないのではっきりとした正規分布かは判別できませんが、正規分布に近い分布ではありそうです。

また、今回のモデルデータではしっかり規格値以内に測定値が収まっていることがわかります。

③工程能力指数を計算・区間推定する

次に工程能力指数と区間推定値を計算します。

工程能力指数を計算するためにはカイ2乗値と標準偏差が必要です。カイ2乗値はscipyを、標準偏差はnumpyを使って計算しましょう。

３６行目からが工程能力指数の計算過程になります。

それでは左側にある「▶︎ボタン」を押してみましょう。

計算してみると現時点のデータ数（N30）における工程能力指数は1.40となり、十分な工程能力指数であることを確認できました。

また、今回はスモールデータだったため工程能力指数を区間推定してみると工程能力指数の区間推定の最大値は1.76, 最小値は1.04となりました。

この結果から、N数を増やして工程能力指数が大きくなれば、真の工程能力はより高い値であるためコストダウンの余地がある、工程能力指数が小さくなれば、真の工程能力はより低い値であるためコストアップする可能性があると考えられるでしょう。

④QCDの観点からリスクの有無を議論する

新製品の性能指標の工程能力を確認したところで、部内で「目標品質を達成できそうか」を議論をします。

新製品の開発段階では、製品コンセプトに応じて得られた工程指数の解釈や取るべきアクションが変わってくるので、過去の記事に書いたように以下のステップを踏むことが重要です。

1. データを見える化する（今まで行ったこと）
2. データをもとにQCDの観点でのリスクの大きさを議論する
3. リスクの大きさに応じて未然防止策を実施する。

先ほどの結果が「重要な検査指標である」と仮定すると、「コストアップを許容して工程能力指数に余裕を持った設計に変更し、実績を確認しながらコストダウンする手法を検討しましょう」とも結論できるでしょう。

まとめ

今回の記事のまとめは以下の通りになります。

1. 工程能力とは「ある工程がどれだけ均一に、どれだけばらつきが小さく製品を生産できるかを示す品質的な能力」を示す。
2. データのばらつきを確認して、正規分布に近い分布をしていることを確認してから工程能力指数を確認する。
3. スモールデータを取り扱うときは、品質検査項目の重要性を照らし合わせながら、設計仕様見直しの必要性を議論する。

更にPythonを使うことで一気通貫で工程能力の計算をすることができるようになりました。

一方で、工程能力指数の算出よりも大事なことは「目標品質を達成できそうか」を議論して品質問題を未然に防ぐことです。

是非、工程能力を計算するだけではなく「品質問題の未然防止」に役立てる議論を進めていただけると幸いです。

以下に本記事を作るのに参考とした書籍を紹介します。

統計学、QCの勉強におすすめの書籍ですので、「QCの知識をより高めたい！」という人はぜひ以下の書籍を読んで勉強していただけると筆者の励みになります。

それでは最後に、私の大好きなドラえもんの言葉で今日の記事を締めさせていただきたいと思います。

---

「なやんでるひまに、一つでもやりなよ」

— ドラえもん

---