【QC検定1級対策】多変量解析の理論と実践③〜Pythonで行う主成分分析〜｜アドラーのQC技術研究所

こんにちは、アドラーです！

今回は「QC検定の実務応用」として、「多変量解析の理論と実践③〜Pythonで行う主成分分析〜」という記事を書きました。

QC検定1級の合格体験談で紹介したようにQC検定1級に合格するためには30分で750字の作文を書く必要があり、QCの本質を理解し、実務活用の経験を積むことが重要です。

一方で、体系的なQC知識は書籍で学ぶことはできても中々その知識を実務に適用することが難しいと感じている方も多いのではないでしょうか。

そこで今回は、製品開発を5年以上続けている研究開発職の私が多変量解析、特に主成分分析の解説からQC検定1級での論文例も紹介します。

主成分分析を使いこなすことができれば、多変数のデータ分析において効率的な次元削減が可能となります。

是非、本記事を読むことで、QC検定1級の論文問題を書くためのヒントを得ていただきながら、皆様のQC知識を実務に活かし、品質トラブルの解決やキャリア形成の方向性を考えるきっかけにしていただけると幸いです。

※本記事は以下の図書を参考に作成しております。品質管理の勉強をしたい方はぜひ以下のリンクから購入ください！（楽天だと0,5のつく日に楽天ポイントが5倍になり、お得に購入ができます！）

トヨタ必須の17の品質管理手法を伝授品質の教科書 [ 皆川一二 ]

楽天ブックス

¥2,970 （2025/04/27 13:12時点 | 楽天市場調べ）

Amazon

楽天市場

ポチップ

東京大学のデータサイエンティスト育成講座 Pythonで手を動かして学ぶデータ分析／中山浩太郎／塚本邦尊／山田典一【3000円以上送料無料】

bookfan 1号店楽天市場店

¥3,278 （2025/04/27 10:52時点 | 楽天市場調べ）

Amazon

楽天市場

ポチップ

アドラー

筆者のプロフィール・ブログ運営の理念は自己紹介からご覧ください！

概要

多変量解析は複数の説明変数から目的変数を予測したり、データの構造を要約することが可能になる。

多変量解析の一つである主成分分析では、多くの変数をできる限り情報のロスがないように要約し、サンプルのグルーピングすることができる。

QC検定1級の論文試験で主成分分析に関する論述をする場合、①主成分分析をする動機を明確にすること、②データの全体像・主成分分析の実施・データの解釈の3点セットを記入すること、③今後の抱負について記述することが重要。

それでは一緒に勉強していきましょう！

主成分分析とは？

前の記事で紹介しましたが、判別分析は多変量解析の一つです。判別分析の説明に移る前に多変量解析を復習しましょう。

多変量解析では、互いに関係する多種類のデータの関係性を整理し、将来の数値の予測をしたり、要約したりするために使う統計的データ解析の総称です。

多変量解析は主に3つの利用シーンに応じて適切な手法を使い分けます。

今回紹介する主成分分析では、多次元の変数の傾向を捉えるために変数を少なくする（次元削減する）手法になります。

利用場面	手法
多数の説明変数に対する量的な目的変数の因果関係を明らかにして、目的変数を予測する。	重回帰分析（説明変数：量的変数）数量化１類（説明変数：カテゴリ変数）
多数の説明変数に対して質的変数（カテゴリ変数）である目的変数との因果関係を明らかにして、未知のサンプルがどのカテゴリに属するかを明らかにする。	判別分析（説明変数：量的変数）数量化２類（説明変数：質的変数）
多くの変数をできる限り情報のロスがないように要約し、サンプルのグルーピングする。 ※目的変数なし	主成分分析（説明変数：量的変数）数量化３類（説明変数：質的変数）

主成分分析の進め方

具体的には以下の手順を踏んで解決案の検討を行います。

解析するデータの収集
関係性を求めたいデータが体系的にまとめられたデータセットを準備する。

データの全体像の把握
散布図行列や要約統計量の確認を行い、データの全体像の確認を行う。

スケーリングと主成分分析の実施
正しい分析ができるようにデータを標準化（スケーリング）し、主成分分析を実施

各種指標の確認
寄与率・各主成分の固有値・各主成分の固有ベクトルを計算する。

各主成分、元変数の関係性の考察
各種成分が何を意味するのか、データを元に考察を行い、QCDの改善に繋げる。

主成分分析用のPythonコード

今回は、前回の記事でも紹介したIris（アヤメ）のデータセットを用いて主成分分析をしてみたいと思います。

分析にはGoogle colaboratoryを用いたいと思います。

Google colaboratoryの全般使い方はこちらのブログにまとまっていましたのでご参考ください。

今回、主成分分析を行なうpythonコードは以下のURLからも見ることができます。

【主成分分析のモデルコード】

https://colab.research.google.com/drive/1ec6WORPNfhkXYmAdV6mWoYPEZC_HZYbm?usp=sharing

ライブラリのインポート

# ライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

Google colaboratoryでは▶︎ボタンを押すとプログラムが動きます。

▶︎マークがチェックマークに変わると思いますがそれで正しくプログラムは動いています。

①データセットの読み込み

# Irisデータセットのロード
# targetは（0: 'setosa', 1: 'versicolor', 2: 'virginica'）
iris = load_iris()
df= pd.DataFrame(data= np.c_[iris['data'], iris['target']],
                       columns= iris['feature_names'] + ['target'])

df.head()

上のコードを動かすとデータのロード、データ格納が始まり、データセットの最初の5行のデータが以下のように表示されます。

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

各変数は以下のような意味です。データの読み込みと各変数の意味を確認できたので、実際にデータの中身を見ていきましょう。

変数名称	意味
sepal length (cm)	がく片の長さ
sepal width (cm)	がく片の幅
petal length (cm)	花弁の長さ
petal width (cm)	花弁の幅

②データの全体像把握

#説明変数の要約統計量を確認
df_iris.describe()

始めに要約統計量を始確認して全体像を確認してみましょう。

データ数、平均値、標準偏差、最小値、25%、50%（中央値）、75%タイルと最大値が出力されました。

今回は細かな分析は行いませんがデータに偏りがあることを念頭に置いて分析を進めていきましょう。

次に散布図行列を作成して、データの全体像をグラフで確認してみましょう。

# 散布図行列を作成
sns.pairplot(df_iris, hue='target',palette="flare")
plt.show()

以上のプログラムを動かすと以下のようなグラフが表示されます。

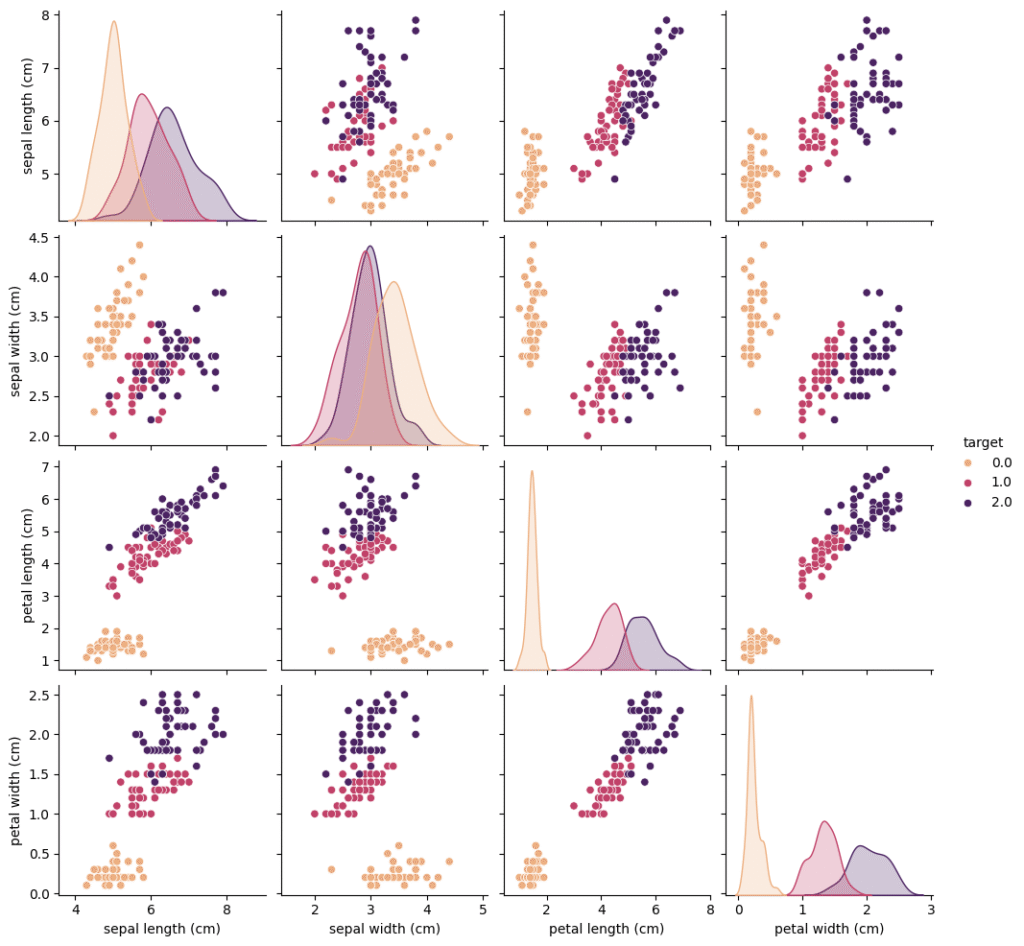
なんとなくデータごとに傾向は持っていて、花弁（petal）の長さや幅によって種類を区別可能でありそうだと予想できます。

③スケーリングと主成分分析の実施

次に実際の主成分分析を行ってみましょう。

主成分分析を行う上で、各変数の単位や数値の大小の意味するところが一致するように標準化処理を行います。

具体的にはデータの各値から変数列の平均値を引き、標準偏差で割ることでスケーリングを行います。

この標準化処理を行うことで、モデルの学習が値の大きな値、低い値に引っ張られてしまうことを防ぐことができます。

# 行列の標準化（各列に対して、平均値を引いたものを標準偏差で割る）
# targetは目的変数であるため今回の解析対象から外します
dfs = df.iloc[:,:4].apply(lambda x: (x-x.mean())/x.std(), axis=0)
dfs.head()

次に主成分分析を行い、主成分得点を実際に見てみます。

# 主成分分析の実行
pca = PCA()
pca.fit(dfs)
# データを主成分空間に写像
feature = pca.transform(dfs)

# 主成分得点を表示
feature=pd.DataFrame(feature, columns=["PC{}".format(x + 1) for x in range(len(dfs.columns))])
feature.head()

主成分得点を計算してみると以下のような結果が得られました。

	PC1	PC2	PC3	PC4
0	-2.257141	0.478424	0.127280	-0.024088
1	-2.074013	-0.671883	0.233826	-0.102663
2	-2.356335	-0.340766	-0.044054	-0.028282
3	-2.291707	-0.595400	-0.090985	0.065735
4	-2.381863	0.644676	-0.015686	0.035803

このままだと結果がよくわからないので、Irisが正しく分類できているかを確認可能な散布図行列を作成してみましょう。

#目的変数（Irisの種類）と主成分データの紐付け
target= pd.DataFrame(data= iris['target'], columns= ['target'])
df_con=pd.concat([feature, target],axis=1)
df_con.head()

# 散布図行列を作成
sns.pairplot(df_con, y_vars="PC1",hue='target',palette="flare")
plt.show()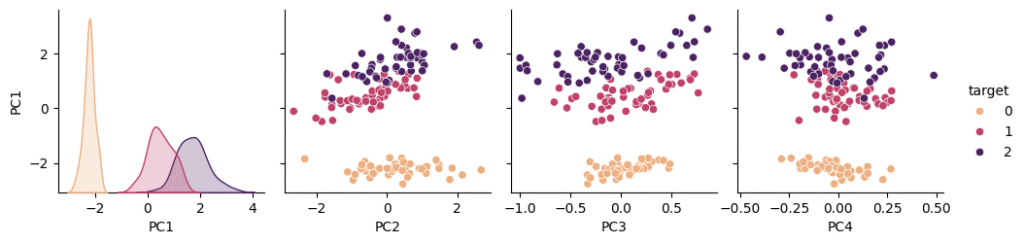

散布図行列を作成してみると左から二つ目の散布図を見てわかるようにPC1とPC2でほとんどのデータが分類できていることがわかりました。主成分分析はうまくできていそうです。

次にこの主成分が意味するところを考察するために各指標を計算してみましょう。

④各種指標の確認

各主成分の固有ベクトル・寄与率・各主成分の固有値・を計算しましょう。

固有ベクトル

# PCA の固有ベクトル
pd.DataFrame(pca.components_, columns=dfs.columns, index=["PC{}".format(x + 1) for x in range(len(dfs.columns))])

固有ベクトルとは、主成分分析により発見された新しい特徴空間の軸の向きを表します。
固有ベクトルの意味を直観的に把握することは難しいですが、数学的には重要な意味を持っているのでしっかり計算しておきましょう。

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
PC1	0.521066	-0.269347	0.580413	0.564857
PC2	0.377418	0.923296	0.024492	0.066942
PC3	0.719566	-0.244382	-0.142126	-0.634273
PC4	-0.261286	0.123510	0.801449	-0.523597

各主成分の分散

次にPCAの固有値（各種成分の分散）を計算しましょう。寄与率を計算することで、データ全体のばらつきはどの主成分由来であるかを判定することができます。

# PCA の固有値（各主成分の分散）
pd.DataFrame(pca.explained_variance_, index=["PC{}".format(x + 1) for x in range(len(dfs.columns))])

主成分	各主成分の分散
PC1	2.918498
PC2	0.914030
PC3	0.146757
PC4	0.020715

計算してみると、PC1の分散が非常に大きく、PC2の主成分が次に大きいです。

つまり、データのばらつきの大半はPC1, PC2で説明できてしまうということを意味しています。

寄与率の計算

次にPCAの寄与率を計算しましょう。

寄与率は各種成分が持つ分散の比率から計算できます。

# 寄与率
pd.DataFrame(pca.explained_variance_ratio_, index=["PC{}".format(x + 1) for x in range(len(dfs.columns))])

主成分	寄与率
PC1	0.729624
PC2	0.228508
PC3	0.036689
PC4	0.005179

先ほどの固有値を元に寄与率を計算されました。

例えば、PC1の寄与率はPC1の固有値/（PC1~4の総和）から算出されます。

この値を元に累積寄与率を計算してみましょう。

# 累積寄与率を図示する
import matplotlib.ticker as ticker
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.xlabel("Number of principal components")
plt.ylabel("Cumulative contribution rate")
plt.grid()
plt.show()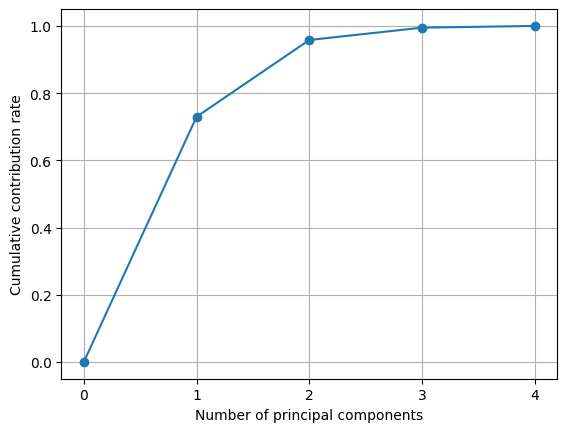

累積寄与率を可視化してみるとPC1,PC2まで次元削除をすることでほとんど全てのデータが説明できることがわかりました。

⑤各主成分、元変数の関係性の考察

次に主成分1,2が何を意味する主成分なのかを分析してみましょう。

# 第一主成分と第二主成分における説明変数の寄与度をプロットする
plt.figure(figsize=(6, 6))
for x, y, name in zip(pca.components_[0], pca.components_, dfs.columns):
    plt.text(x, y, name)
plt.scatter(pca.components_[0], pca.components_, alpha=0.8)
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()

このコードでは、第1、2主成分における説明変数の寄与度をプロットします。

動かしてみると以下のようなプロットが得られました。

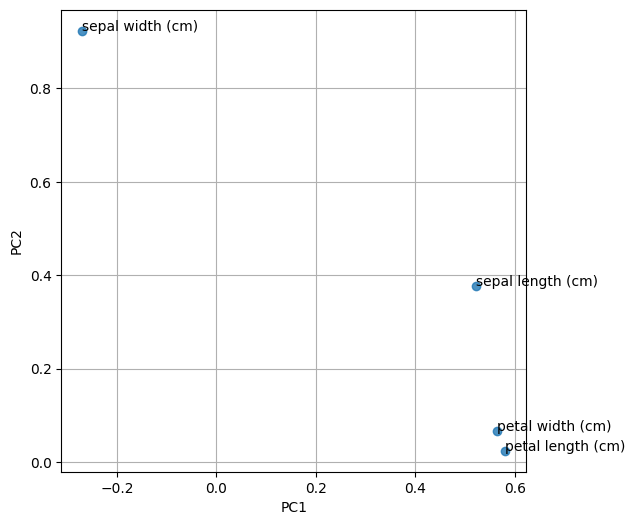
第1主成分は、花弁（petal）の長さや幅、がく片（sepal）の長さの寄与度が正の方向で0.60と特に大きく、この第1種成分のみで8割程度のあやめは区別できることがわかりました。

第2主成分は、がく片（sepal）の幅の寄与度が0.80と特に大きい指標であることがわかりました。第１主成分のみで判別できないデータはがく片（sepal）の幅に注目すれば識別できそうです。

QC検定1級論文について

基本的には重回帰分析の作文例と同様に作文をすれば十分合格点に達すると思います。

過去の出題事例はなく、出題の可能性は低いと思いますが、予想問題と解答例を作成しましたので、是非ご活用ください。

【作文テーマ（制限字数：750字）】

自身の業務で主成分分析を用いた際に、解析の際に注意した点とどのような形でQCDの改善に繋げたかを記述せよ。

※QC検定1級問題を一部改変しました。

作文例（720字）

私は化学メーカーの研究開発業務の実施者である。主成分分析を用いて自社製品のQCDの改善に繋げた事例について記述する。

私は今年から新製品開発を担当する部署に異動し、新製品の開発コンセプトを決定するために顧客にアンケート調査を行った。具体的には、価格、使いやすさ、ブランド、耐久性、機能性の５項目をそれぞれ10点満点で調査し、それぞれの顧客が自社製品に対してどのような印象を持っているか調査した。更に、得られたアンケート結果を整理し、グラフにして視覚化できるように主成分分析を行った。

初めに、得られたデータを散布図行列で可視化し、エラー値がないかを確認した後に主成分分析を行った。固有ベクトル、各種成分の分散、寄与率を計算したところ、主成分1と主成分2の寄与率が特に大きいことがわかった。主成分1と主成分2に対応する説明変数を確認すると以下の2つのグループに大別できることがわかった。

グループ①：機能性、価格、耐久性に魅力を感じているが、使いやすさに少不満を持っている顧客
グループ②：使いやすさに魅力を感じている顧客

以上の結果から、使いやすさは一元的な品質であり、機能性、価格、耐久性とトレードオフにあることが示唆された。今後の製品開発のコンセプトは使いやすさと機能性などの指標とのトレードオフを脱却することであると部内で結論づけた。

今後はこの分析結果を元にして品質機能展開を行い、要求品質と技術要素との対応を明らかにしていく。更に、製造部・品証部・営業部などの関係部署とデザインレビューを行なって技術的な課題と採算性や原材料の調達性などを多角的に議論して、顧客が真に求める品質を確保した製品を、適切なコストとなるように開発を進める予定である。

作文のポイント

①主成分分析をする動機を明確にする。

主成分分析の目的は「多くの変数をできる限り情報のロスがないように要約し、サンプルのグルーピングすること」です。今回は、新製品の開発をするにあたり顧客ニーズを可視化するために用いました。

以上のように主成分分析を行った理由を作文の冒頭に明記することで、審査官が作文の意図を理解しやすくなるので、重回帰分析を行なった動機を必ず記述するようにしましょう。

②データの全体像・主成分分析の実施・データの解釈の3点セットを記入する。

次に、Pythonで示したケーススタディに則り、①データの全体像の把握、②主成分分析および各指標の計算、③データの解釈の3点セットを確認するようにしましょう。

3点セットを行う理由は前章で述べた通りですが、データの予測の信頼性を担保したことを審査官にアピールすることができます。

③今後の抱負について記述する

主成分分析を行った上で、どのような製品開発を行うかを記入して、QCDの改善に繋げていることをアピールしましょう。今回は、顧客ニーズを把握するために主成分分析を行いましたので、この結果をQFD（品質機能展開）における要求品質の定義に用いたことを説明すると良いでしょう。

ぜひこの最適な品質のレシピを上市するために取り組んだこと、もしくはこれから取り組もうとしていることを記述しましょう。

アドラー

基本に忠実に作文をしながら、今後の抱負をしっかり盛り込むことが重要です。

まとめ

記事のまとめは以下のとおりです。

多変量解析は複数の説明変数から目的変数を予測したり、データの構造を要約することが可能になる。

多変量解析の一つである主成分分析では、多くの変数をできる限り情報のロスがないように要約し、サンプルのグルーピングすることができる。

QC検定1級の論文試験で主成分分析に関する論述をする場合、①主成分分析をする動機を明確にすること、②データの全体像・主成分分析の実施・データの解釈の3点セットを記入すること、③今後の抱負について記述することが重要。

更にケーススタディやQC検定1級の作文例から、主成分分析の実施を体験することができました。

是非、本記事のテンプレートを使って主成分分析を行い、既存のデータから優位な情報を見出すことで品質改善に向けた議論を進めていただけると幸いです。

以下に本記事を作るのに参考とした書籍を紹介します。

統計学、QCの勉強におすすめの書籍ですので、「QCの知識をより高めたい！」という人はぜひ以下の書籍を読んで勉強していただけると筆者の励みになります。