【QC検定1級対策】多変量解析の理論と実践②〜Pythonで行う判別分析〜｜アドラーのQC技術研究所

こんにちは、アドラーです！

今回は「QC検定の実務応用」として、「多変量解析の理論と実践②〜Pythonで行う判別分析〜」という記事を書きました。

QC検定1級の合格体験談で紹介したようにQC検定1級に合格するためには30分で750字の作文を書く必要があり、QCの本質を理解し、実務活用の経験を積むことが重要です。

一方で、体系的なQC知識は書籍で学ぶことはできても中々その知識を実務に適用することが難しいと感じている方も多いのではないでしょうか。

前の記事で紹介した重回帰分析と重複する内容が多いですが、重回帰分析と判別分析の違いを学んでいただき、実務への適用に役立てていただけると幸いです。

※本記事は以下の図書を参考に作成しております。品質管理の勉強をしたい方はぜひ以下のリンクから購入ください！（楽天だと0,5のつく日に楽天ポイントが5倍になり、お得に購入ができます！）

トヨタ必須の17の品質管理手法を伝授品質の教科書 [ 皆川一二 ]

楽天ブックス

¥2,970 （2025/04/27 13:12時点 | 楽天市場調べ）

Amazon

楽天市場

ポチップ

東京大学のデータサイエンティスト育成講座 Pythonで手を動かして学ぶデータ分析／中山浩太郎／塚本邦尊／山田典一【3000円以上送料無料】

bookfan 1号店楽天市場店

¥3,278 （2025/04/27 10:52時点 | 楽天市場調べ）

Amazon

楽天市場

ポチップ

アドラー

筆者のプロフィール・ブログ運営の理念は自己紹介からご覧ください！

1 概要
2 （復習）多変量解析とは？
3 重回帰分析と判別分析の違い
4 判別分析の進め方
5 判別分析用のPythonコード
6 まとめ

概要

多変量解析は複数の説明変数から目的変数を予測したり、データの構造を要約することが可能になる。

多変量解析の一つである判別分析では、多くの説明変数と一つの目的変数（カテゴリ変数）の因果関係を求め、目的変数を予測したい場合に有効である。

それでは一緒に勉強していきましょう！

（復習）多変量解析とは？

前の記事で紹介しましたが、判別分析は多変量解析の一つです。判別分析の説明に移る前に多変量解析を復習しましょう。

多変量解析では、互いに関係する多種類のデータの関係性を整理し、将来の数値の予測をしたり、要約したりするために使う統計的データ解析の総称です。

多変量解析は主に3つの利用シーンに応じて適切な手法を使い分けます。

利用場面	手法
多数の説明変数に対する量的な目的変数の因果関係を明らかにして、目的変数を予測する。	重回帰分析（説明変数：量的変数）数量化１類（説明変数：カテゴリ変数）
多数の説明変数に対して質的変数（カテゴリ変数）である目的変数との因果関係を明らかにして、未知のサンプルがどのカテゴリに属するかを明らかにする。	判別分析（説明変数：量的変数）数量化２類（説明変数：質的変数）
多くの変数をできる限り情報のロスがないように要約し、サンプルのグルーピングする。 ※目的変数なし	主成分分析（説明変数：量的変数）数量化３類（説明変数：質的変数）

重回帰分析と判別分析の違い

前項で述べたように、重回帰分析は説明変数も目的変数も量的な変数であることが特徴です。判別分析は説明変数が量的変数であるのは同じですが、目的変数が質的変数（カテゴリー）であることが異なります。

手法	説明変数	目的変数	事例
重回帰分析	複数の量的変数	量的変数	野球の勝率予測
判別分析	複数の量的変数	質的変数（カテゴリ変数）	健康診断の検査値から健常者\|患者を判別

例えば、判別分析では、健康診断の各検査値を元に受診者が健常者なのか、要治療の患者なのか所属するカテゴリを判別するイメージです。

前の記事で説明した重回帰分析を野球に適用しようとするとチーム打率と防御率、本塁打、出場メンバーの体調などから勝率（量的変数）を予測するイメージです。

判別分析の進め方

前の記事で確認した重回帰分析と同様に判別分析の流れを確認しましょう。

具体的には以下の手順を踏んで検討を行いますが、基本的には重回帰分析と同様です。

解析するデータの収集
関係性を求めたいデータが体系的にまとめられたデータセットを準備する。

データセットを説明変数と目的変数へ分割

判別分析の実施と決定係数の確認
判別分析を行い、確からしい予測ができているかを決定係数を元に確認する。

（必要があれば）新たなデータをデータセットに加えていき、予測精度を高めてみる。

判別分析用のPythonコード

今回は、scikit-learnサイトで公開されている「アヤメのデータセット」を使って簡単な重回帰分析をしてみます。

Google colaboratoryの全般使い方はこちらのブログにまとまっていましたのでご参考ください。

今回、重回帰分析を行なうpythonコードは以下のURLからも見ることができます。

【判別分析のモデルコード】

https://colab.research.google.com/drive/1Lq4pFx0vfVH3x1nuAhfKTCHfr0uvhATi?usp=sharing

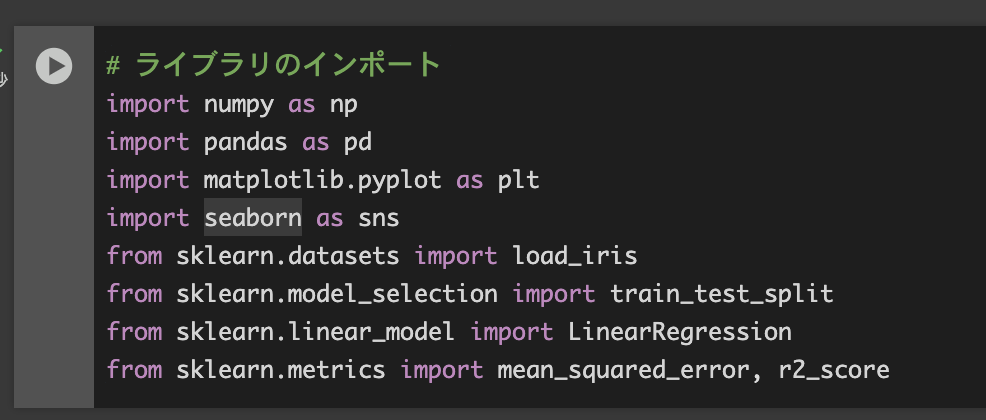
①ライブラリのインポート

# ライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

Google colaboratoryでは以下のような画像が出ていると思いますが、▶︎ボタンを押すとプログラムが動きます。▶︎マークがチェックマークに変わると思いますがそれで正しくプログラムは動いています。

②データセットの表示と確認

# Irisデータセットのロード
# targetは（0: 'setosa', 1: 'versicolor', 2: 'virginica'）
iris = load_iris()
df_iris = pd.DataFrame(data= np.c_[iris['data'], iris['target']],
                       columns= iris['feature_names'] + ['target'])

df_iris.head()

上のコードを動かすとデータのロード、データ格納が始まり、データセットの最初の5行のデータが表示されます。

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

各変数は以下のような意味です。データの読み込みと各変数の意味を確認できたので、実際にデータの中身を見ていきましょう。

変数名称	意味
sepal length (cm)	がく片の長さ
sepal width (cm)	がく片の幅
petal length (cm)	花弁の長さ
petal width (cm)	花弁の幅

#説明変数の要約統計量を確認
df_iris.describe()

始めに要約統計量を始確認して全体像を確認してみましょう。

データ数、平均値、標準偏差、最小値、25%、50%（中央値）、75%タイルと最大値が出力されました。

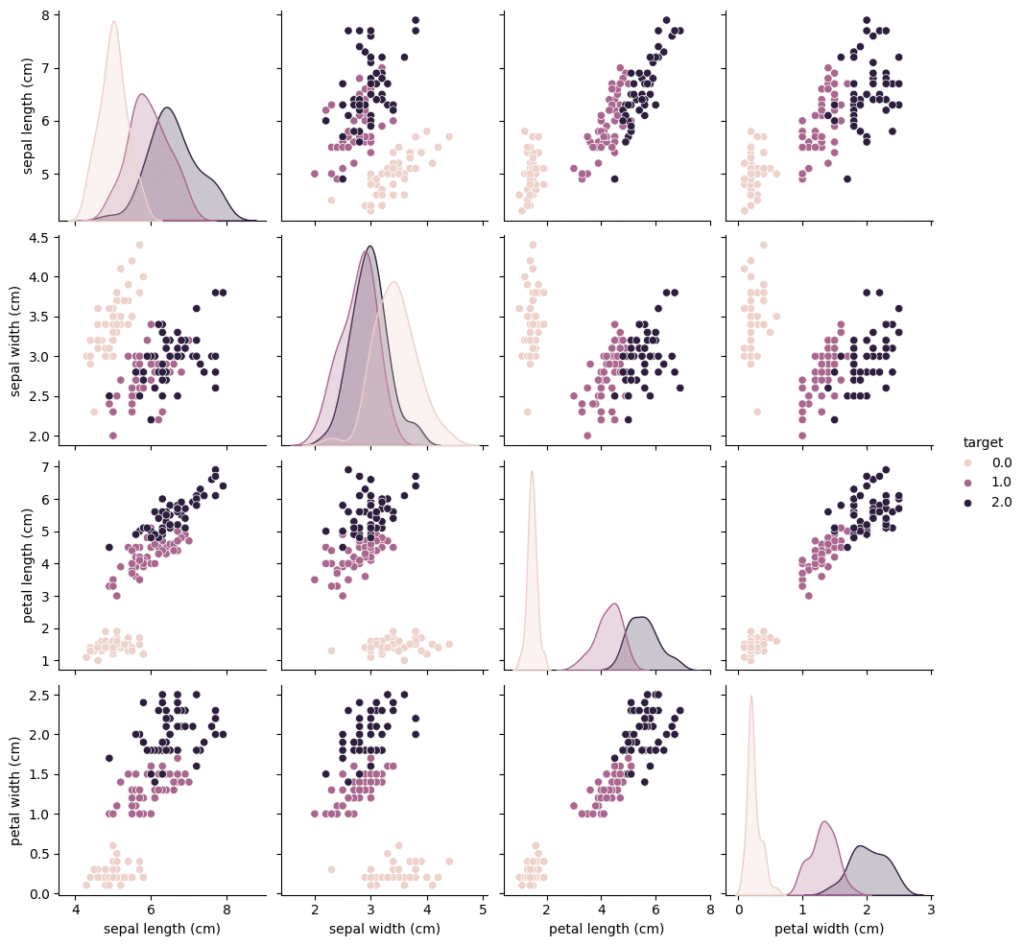
# 散布図行列を作成
sns.pairplot(df_iris, hue='target')
plt.show()

先ほどの要約統計量だけではデータの全体像が捉え切れないので、次は散布図行列を用いて可視化してみましょう。

先ほどの要約統計量よりもデータの全体像が捉えやすくなりました。

例えば、targetの0（setosa）が全体的に短いがく片、花弁を持っているなど、一定の傾向を示していることがわかります。

# 相関行列を計算
corr = iris_df.drop('target', axis=1).corr()

# ヒートマップを作成
sns.heatmap(corr, annot=True)
plt.show()

先ほどの散布図行列で全体像を捉えられたので、相関係数を行列形式で確認してみましょう。

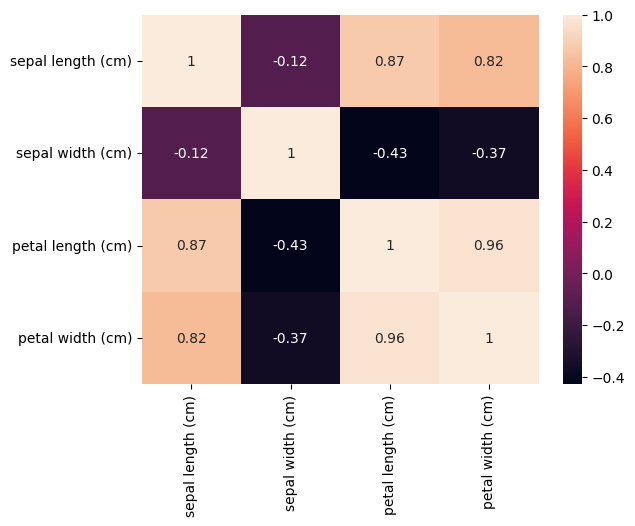
花弁の幅と長さの相関係数が0.96と特に高いことがわかりました。

前回の重回帰分析の記事で述べたように多重共線性の問題がありそうですが、今回は、実験なのでそこまで厳密に考えずにモデル構築をするようにします。

③説明変数と目的変数への分割

# データとラベルを準備
X = iris.data
y = iris.target

# 訓練セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

データの全体像を確認したところで、実際の判別分析に着手します。

上記のコードでデータセットを説明変数と目的変数に分けます。アヤメの種類が目的変数y, そのほかの変数を説明変数xとします。

④判別分析と決定係数の確認

# モデルの訓練
model_lr = LogisticRegression(max_iter=200)
model_lr.fit(X_train, y_train)

# 決定係数を表示
print('決定係数(train):{:.3f}'.format(model_lr.score(X_train,y_train)))
print('決定係数(test):{:.3f}'.format(model_lr.score(X_test,y_test)))

今回は最も一般的な判別分析のアルゴリズムであるロジスティック回帰で回帰をしてみます。回帰分析は上記のコードで終了します。

解析の結果として以下の結果が出力されました。